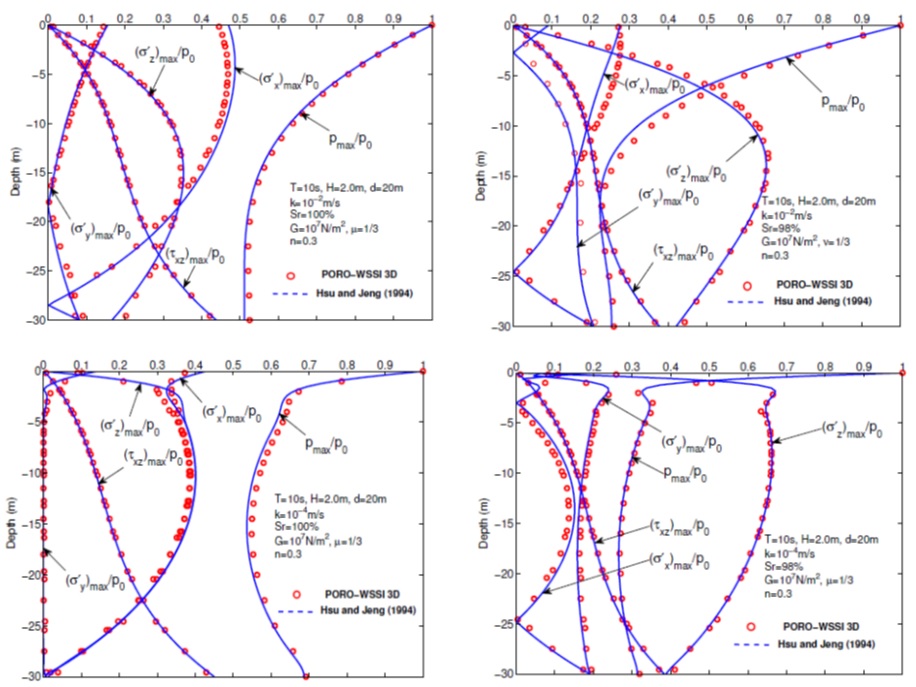
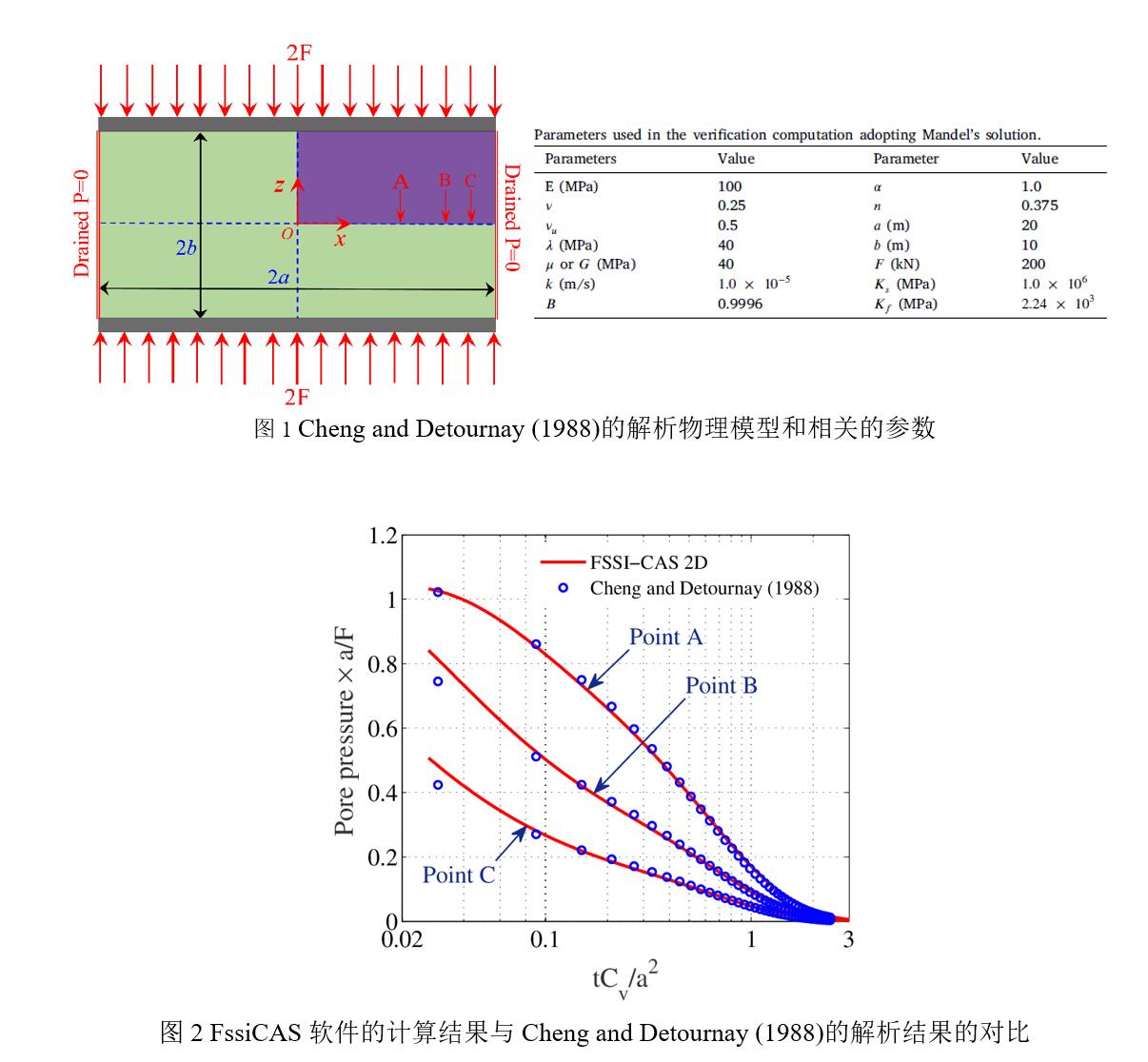
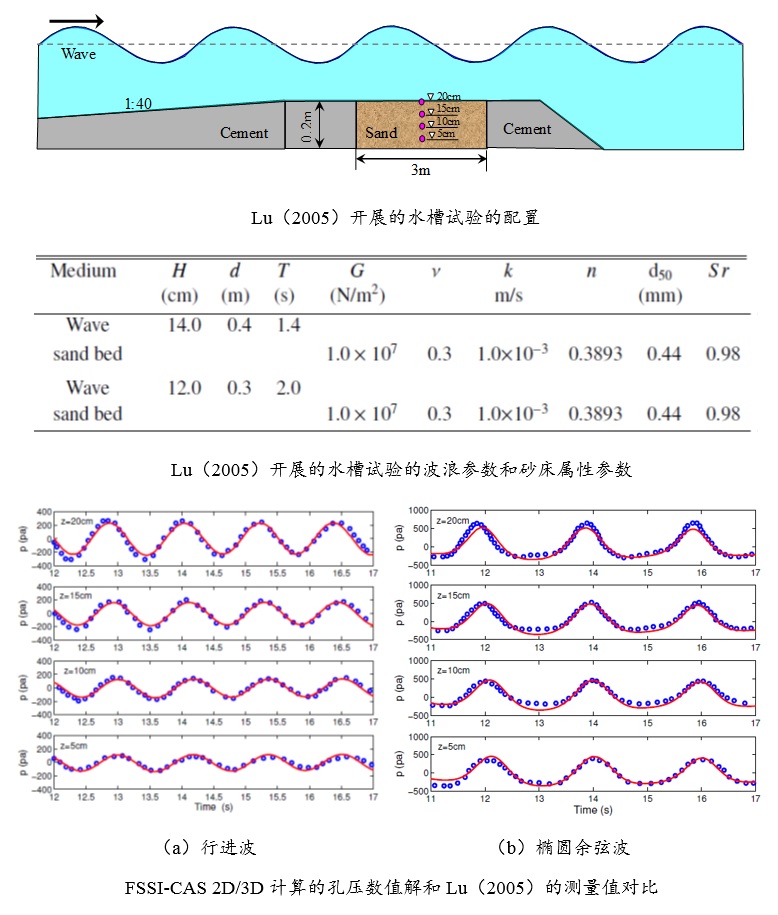
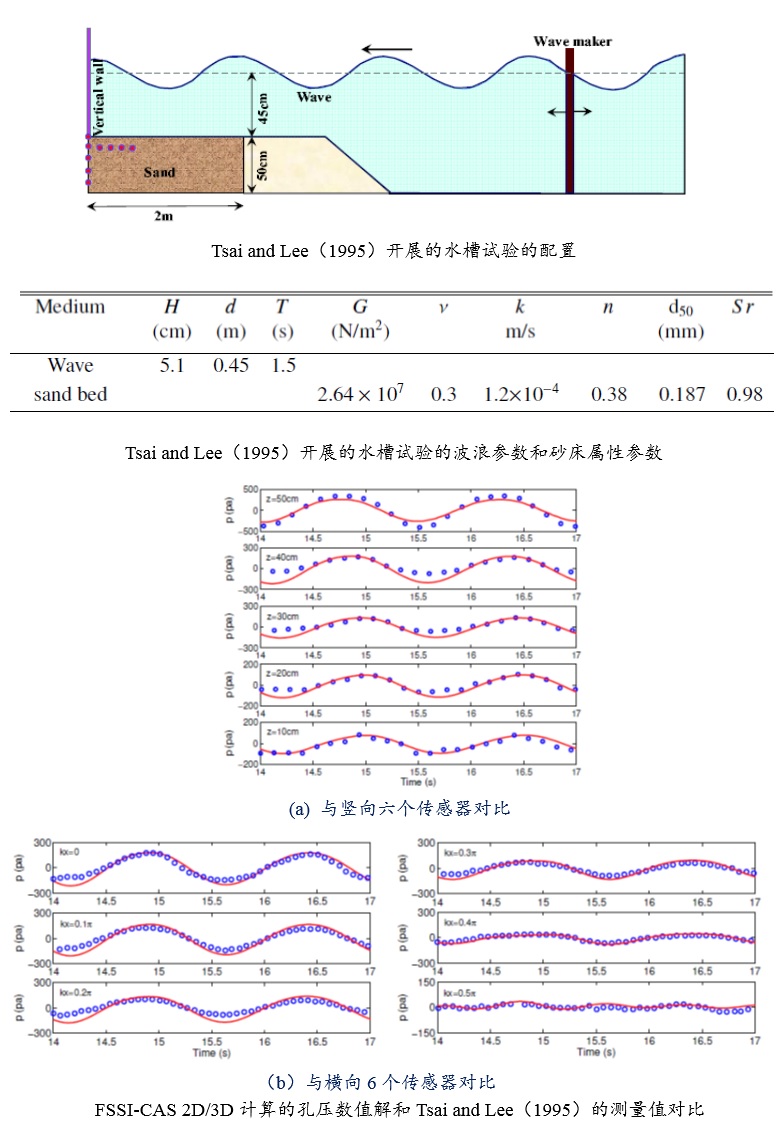
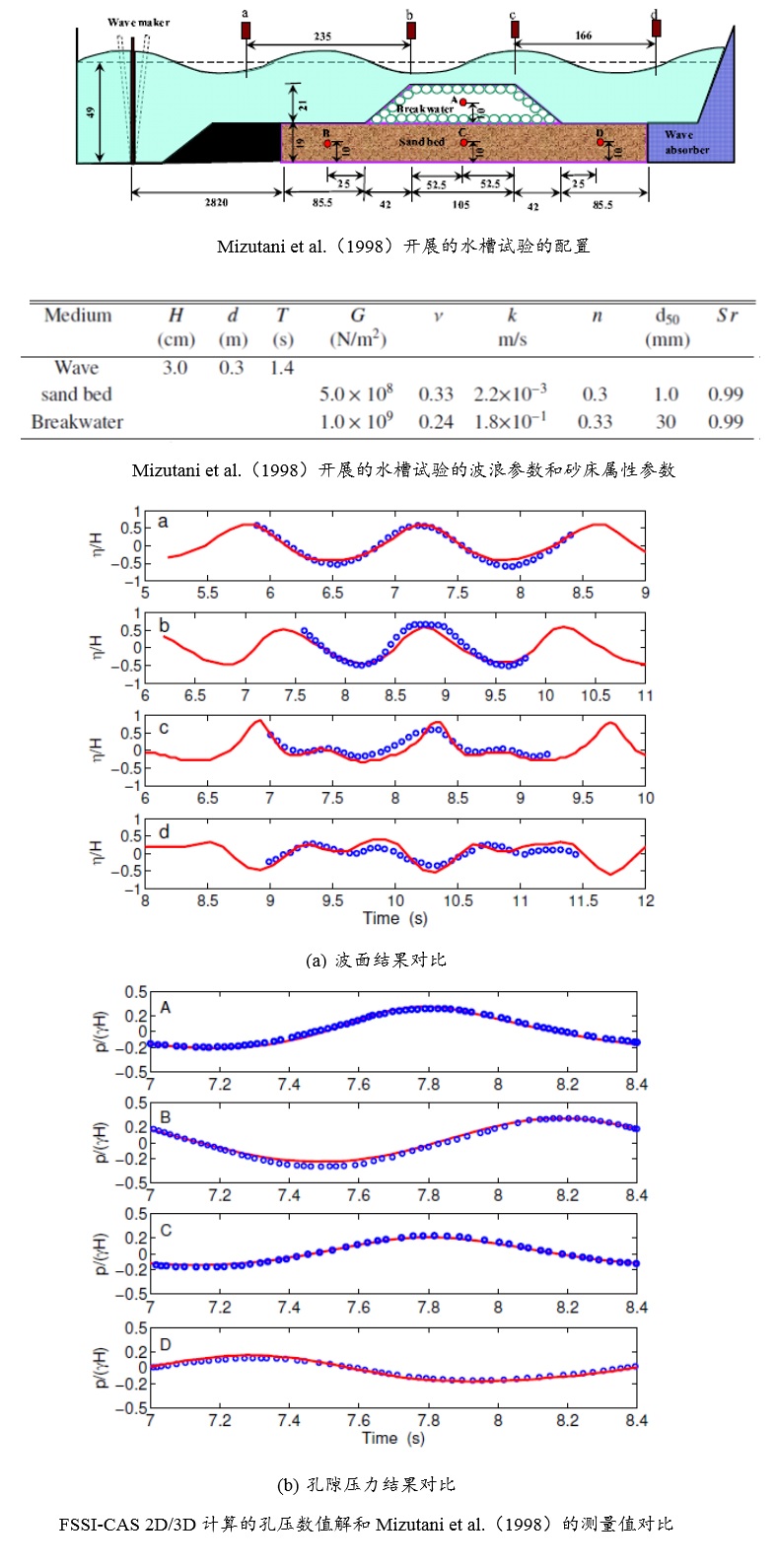
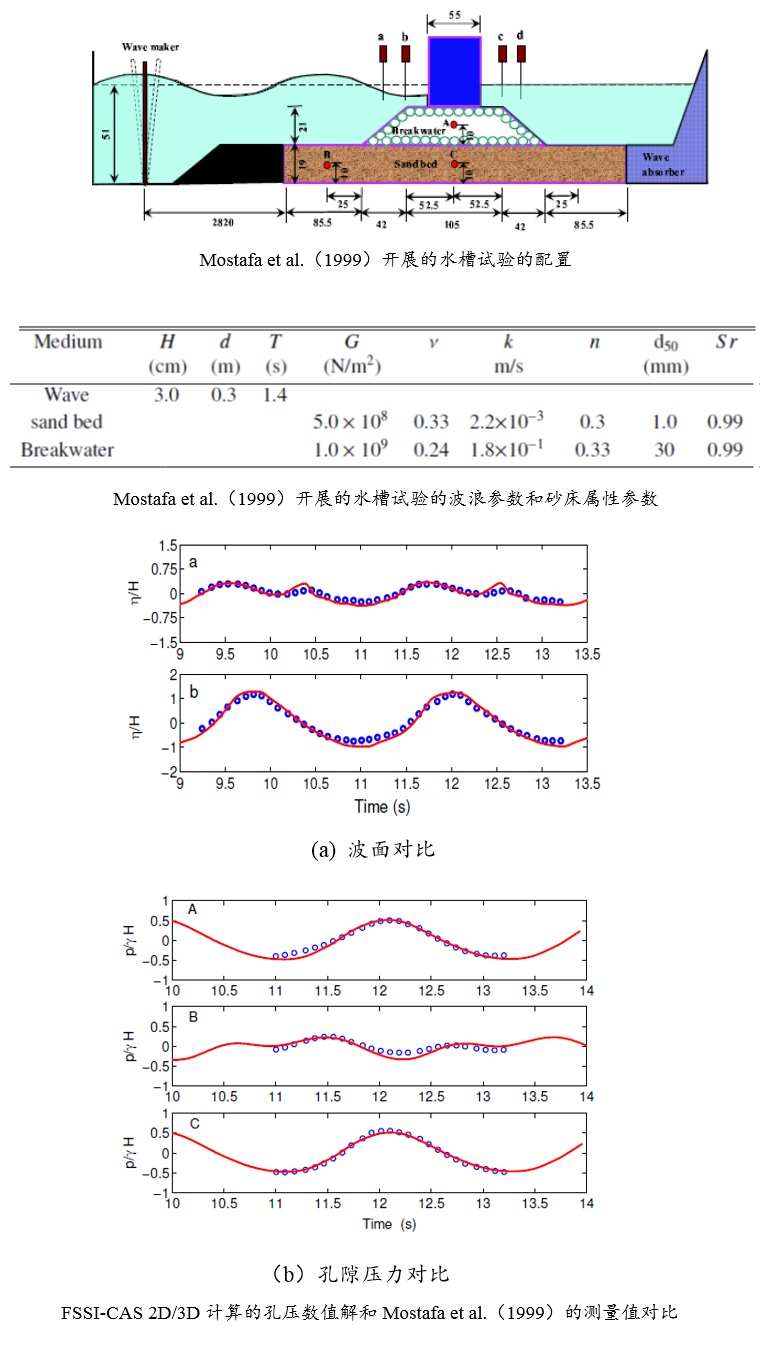
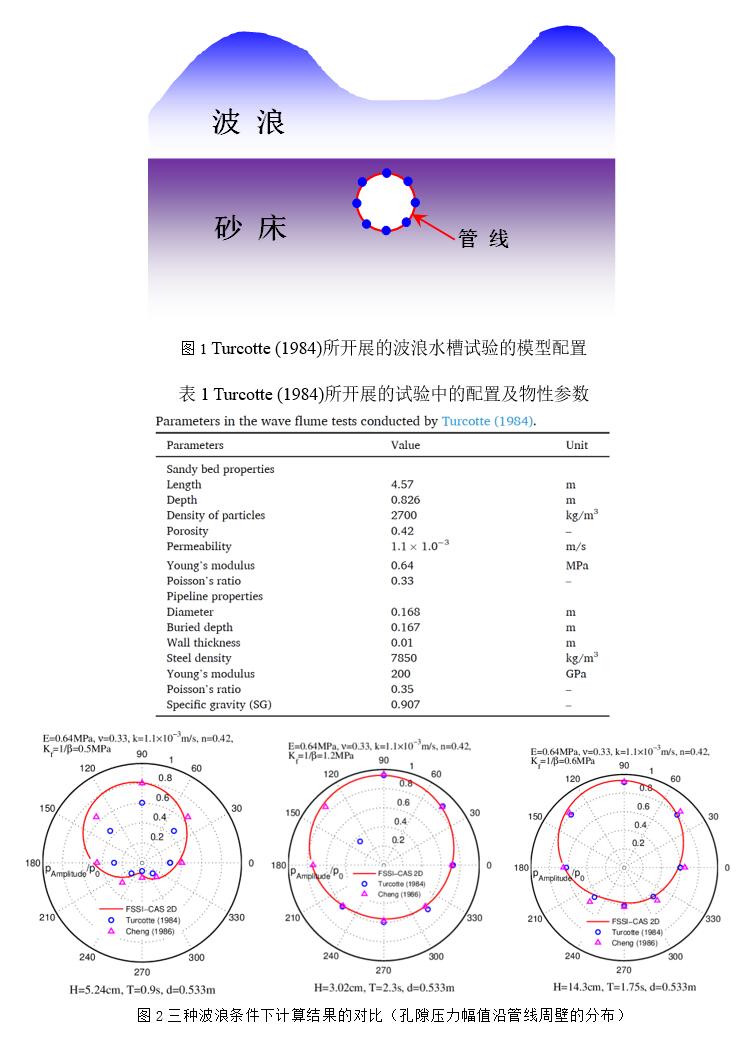
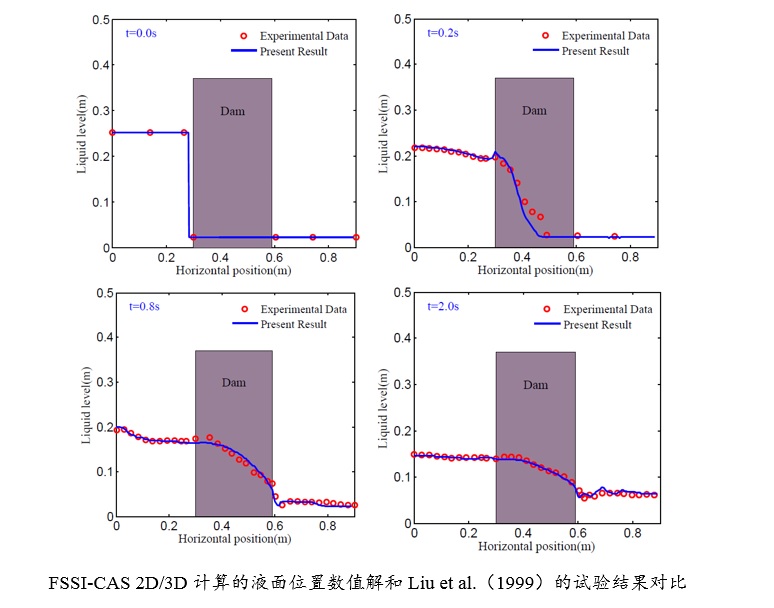
Tsai and Lee(1995)针对反射驻波在平直密实弹性海床上传播时导致的海床应力和孔隙压力变化规律,开展了水槽试验;试验中在水槽一侧采用推板造波机造波,在水槽另一侧砂床末端放置一块坚硬板子,用以反射入射波在板前形成驻波。采用竖向排列的5个孔隙压力传感器(在板子下方),以及水平方向6个孔隙压力传感器测量砂床内部水压力对驻波的动态响应。采用FssiCAS耦合模型重现了Tsai and Lee(1995)所开展的物理水槽试验,得到波浪传播过程中砂床内孔隙压力的数值解;并将FssiCAS的数值解和Tsai and Lee(1995)试验结果进行对比,发现耦合模型FssiCAS具有很好的准确性和可靠性。